Ctrl+K

Introduction to PyMC

%matplotlib inline
import re as re
import pandas as pd
import numpy as np
import seaborn as sbn
from scipy.stats import norm
import matplotlib.pyplot as plt

sbn.set_style('white')
sbn.set_context('talk')

np.random.seed(12345678)

Introduction to PyMC#

Note

Note: the description of software in this introduction are my personal opinions and I’m sure that lots of people would disagree with my assessment of available software packages.

We have been working on getting under the hood of Metropolis-Hastings and Monte Carlo Markov Chain. But there are some very accessible Metropolis Markov Chain software packages out there. These are my personal views on what is available:

  1. Stata (bayesianmh)- just available in Stata 14. To be honest, I have never heard of anyone using Stata for Bayesian Sampling Methods although I haven’t really looked.

  2. Matlab. There are numerous user and Matlab written routines. For example, there is a version of emcee that is implemented there (more on this later in the course). Matlab is for people who want to possibly tweak their own sampler code and who need the fastest possible computation.

  3. SAS. A decent set of packages, not used very much in the social sciences (maybe in the medical sciences??), but is well suited for big data.

  4. R. For a long time R was the de-facto standard and probably still is, with packages like R-stan which interfaces the STAN C Library. Another big advantage to using R-stan is that Gelman is an active contributer to that package. Also Jags, Rbugs and Open BUGS have been around for a long time. I almost elected to teach this course in R.

  5. Python. The libraries aren’t as rich as R, but you might view Python as sitting between Matlab and R. Maybe (in my view probably) faster and also easier to code your own samplers than R. Python is the de facto language for many applied physicists, and they need speed and the latest samplers. Additionally Python is strong in the big-data environment, more so than any of the other packages mentioned above. The major players on python are:

    • PyMC

    • PyStan

    • EMCEE

    • Tensorflow Probability

    • PyTorch

    • Jax (not exactly a Bayesian library, but often useful)

These final three packages are also optimized to use graphical processors (GPUs) which can result in massive speedups for computationally expensive models.

Today, we are going to focus on PyMC, which is a very easy to use package now that we have a solid understanding of how posteriors are constructed.

We will start with our very simple one parameter model and then move to slightly more complicated settings:

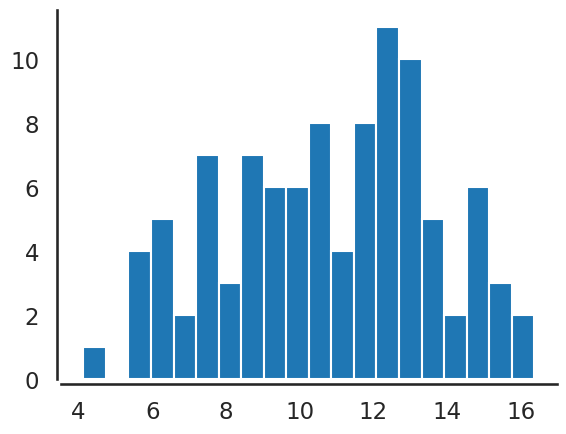
sigma = 3 # Note this is the std of our data
data = norm(10,sigma).rvs(100)

# hyperparameters on prior for mu
mu_prior = 8
sigma_prior = 1.5

plt.hist(data,bins=20)
sbn.despine(offset=3.)
plt.show()
../_images/2107ca74ce989a4f6d31c4a512ea18878eec405e50eeca578c51dc2e91b18c87.png

PyMC#

Let’s use PyMC to model this:

This is the model statement describing priors and the likelihood. Here, mu is defined as a stochastic variable (we want a chain of sampled values for this variable) and we provide a prior distribution and hyper-parameters for it. The likelihood function is chosen to be Normal, with one parameter to be estimated (mu), and we use known \(\sigma\) (denoted as sigma). Our “dependent variable” is given by observed=data, where data is generated above and shown in the histogram. In more formal terms, the code below sets up a basic_model having the following form:

(3)#\[\begin{align} Prob(\mu|\sigma,\mathbf{data}) \propto& Prob(\mathbf{data}|\mu,\sigma) \times Prob(\mu | \mu^0_\mu, \sigma^0_\mu) \nonumber \\ Prob(\mu|\sigma,\mathbf{data}) \propto& \phi \left( \frac{\mathbf{data} - \mu}{\sigma} \right ) \times \phi \left(\frac{\mu - \mu^0_\mu}{\sigma^0_\mu} \right ) \nonumber \\ Prob(\mu|\sigma,\mathbf{data}) \propto& \phi \left( \frac{\mathbf{data} - \mu}{3} \right ) \times \phi \left(\frac{\mu - 8}{1.5} \right ) \end{align}\]

where \(\phi(.)\) is the standard normal pdf.

This code sets up the model (with name basic_model) but doesn’t sample from it:

import pymc as pm

with pm.Model() as basic_model:

    # Priors for unknown model parameters
    mu = pm.Normal('Mean of Data',mu_prior,sigma_prior)
    
    # Likelihood (sampling distribution) of observations
    data_in = pm.Normal('Y_obs', mu=mu, sigma=sigma, observed=data)

The following uses our PyMC model and proceeds with sampling. We will set starting values at MAP and use a Metropolis step method (which is Random Walk MH that we have studied so far).

chain_length = 10000 

with basic_model:
    # obtain starting values via MAP
    startvals = pm.find_MAP(model=basic_model)
    print(startvals)
    # instantiate sampler
    step = pm.Metropolis() 

    # draw posterior samples
    trace = pm.sample(chain_length, step=step, initvals=startvals, tune=1000,
                       return_inferencedata=True, progressbar=False)
100.00% [3/3 00:00<00:00 logp = -290.67, ||grad|| = 31.153] 


{'Mean of Data': array(10.69594596)}

Multiprocess sampling (2 chains in 2 jobs)

Metropolis: [Mean of Data]

Sampling 2 chains for 1_000 tune and 10_000 draw iterations (2_000 + 20_000 draws total) took 2 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

A few things to note about this code

  1. We will tune and burn-in our sampler using the first 1000 samples. Note the option discard_tuned_samples by default is set to True. Therefore our sampler is actually sampling 11,000 times but only returning 10,000.

  2. We are starting our chain using MAP. This may or may not be a good idea depending on your problem. If we don’t supply starting values,PyMC makes intelligent decisions about starting values.

  3. We are using random-walk Metropolis Hastings using the Metropolis() step method. This method auto-tunes the proposal width and discards the samples during the tuning process (first 1000 samples).

  4. Note that the sampler automatically samples multiple independent chains (for Gelman-Rubin convergence criteria). By default 4 cores are sampled unless there are fewer processor cores available (in which case the number of samples is equal to the number of cores, but no less than 2).

In addition to having an easy way to setup and sample from a model without having to write the accept/reject algorith, PyMC offers a full suite of tools for visualizing and assessing the convergence properties of your chain.

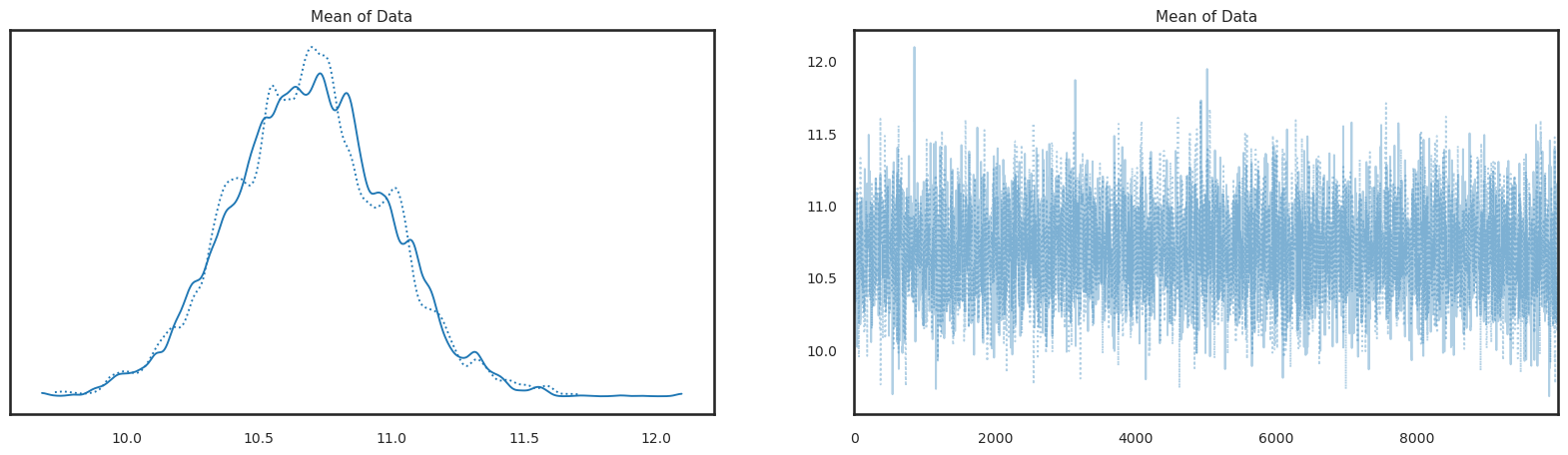
  • Visualize the traces. For each of the four chains:

pm.plot_trace(trace,figsize=(20,5));
../_images/3c6e4f871f15fa0986dd4e65e8ceb28845309e0ca4e0910e23570fa8b6785989.png

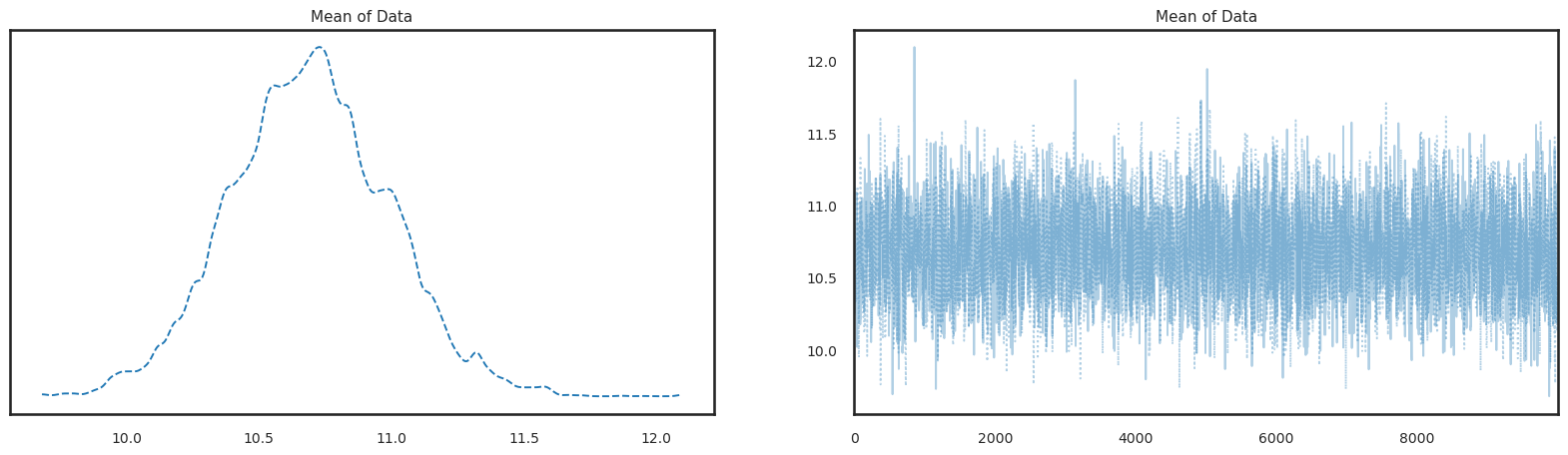
or we can combine all information for the histogram on the left panel (visualization of the posterior) across all chains

pm.plot_trace(trace, figsize=(20,5), combined=True);
../_images/83ec97e503ea8d58b8532500a5b8ad24e9f300eb3b0c36cdc06842668a95bb9f.png

  • Summarize the posterior. Note by default, this combines samples across all chains:

pm.summary(trace)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
Mean of Data 10.69 0.297 10.104 11.215 0.005 0.003 3783.0 4091.0 1.0

Note, that the summary has useful convergence criteria for each parameter (r_hat) is the Gelman Rubin statistic, and the effective sample size measures are given by ess_bulk and ess_tail.

Understanding the PyMC Results Object#

All the results are contained in the trace variable. Since in the above pm3.sample call, we specified inference_data=True, this returns and Arviz inference data. What you need to know about this is that it is a data standard for multiple Bayesian software packages and understanding the structure of this object is useful in numerous ways.

First, notice that the object organizes information for our simple model around the following keys (identifiers):

trace.keys()

KeysView(Inference data with groups:
	> posterior
	> sample_stats
	> observed_data)

For our purposes, the posterior and sample_stats are the most important items to focus on. Look inside the object to examine the estimated mean inside the posterior:

trace.posterior

<xarray.Dataset>
Dimensions:       (chain: 2, draw: 10000)
Coordinates:
  * chain         (chain) int64 0 1
  * draw          (draw) int64 0 1 2 3 4 5 6 ... 9994 9995 9996 9997 9998 9999
Data variables:
    Mean of Data  (chain, draw) float64 10.78 10.78 10.78 ... 10.51 10.51 10.51
Attributes:
    created_at:                 2024-01-12T10:52:02.605841
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.10.3
    sampling_time:              2.3172712326049805
    tuning_steps:               1000

Further we can drill down to examine only the sampled Mean of Data parameter:

trace.posterior['Mean of Data']

<xarray.DataArray 'Mean of Data' (chain: 2, draw: 10000)>
array([[10.78335751, 10.78335751, 10.78335751, ..., 10.31184733,
        10.31184733, 11.17041015],
       [10.66553476, 10.66553476, 10.86596014, ..., 10.5130954 ,
        10.5130954 , 10.5130954 ]])
Coordinates:
  * chain    (chain) int64 0 1
  * draw     (draw) int64 0 1 2 3 4 5 6 7 ... 9993 9994 9995 9996 9997 9998 9999

Notice that the name each parameter tracked inside the posterior is exactly as specified in the pymc model. If you want to extract your samples and place them in a numpy array, use

trace_np = trace.posterior['Mean of Data'].to_numpy()

This trace has the following shape:

trace_np.shape

(2, 10000)

Where the first dimension is the number of chains, and the second is the number of samples per chain.

Selecting subsets of chains/samples from the Inference Data object#

Sometimes you want to

  1. Only examine a single chain, or

  2. Omit burn-in observations

Before running diagnostics or visualizing the results. The sel method is useful in this regard. Suppose we only want to visualize a single chain:

pm.plot_trace(trace.sel(chain=[0]));
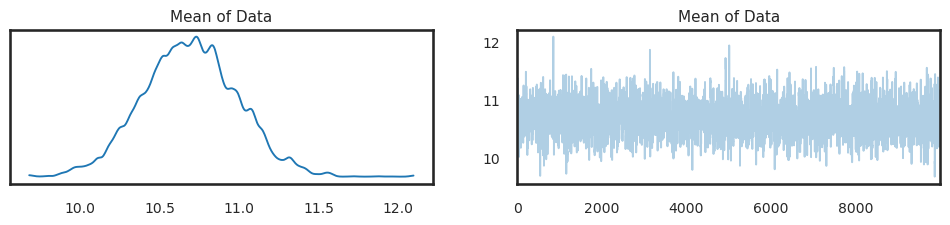
../_images/61ba5ed47088af619d47e7d92255d936ab9d37929829853411c6d7060001b7dc.png

This performs a trace plot over only the first chain, rather than over all of them. One can also “drop” samples if you need longer burn-in:

keep_samples = [i for i in range(5000,10000)]
trace_burn_in = trace.sel(draw=keep_samples)
pm.plot_trace(trace_burn_in);
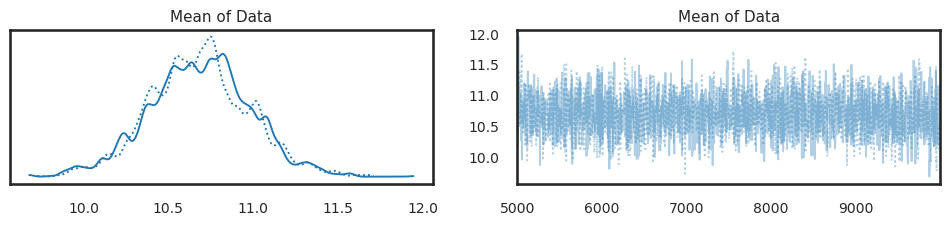
../_images/01aaae165a63d9d65dc72269f368800ca7aec86ea6bbd86afd77eb08fcaf4120.png

This shows a traceplot for the last 5000 samples for each chain (dropping the first 5000). Using similar techniques, we can also compute summaries only on these last 5000 samples:

pm.summary(trace_burn_in)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
Mean of Data 10.685 0.294 10.104 11.207 0.007 0.005 2013.0 2019.0 1.0

Diagnostics#

Many of the key diagnostics discussed in the previous chapter are already included in the summary call:

pm.summary(trace)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
Mean of Data 10.69 0.297 10.104 11.215 0.005 0.003 3783.0 4091.0 1.0

Note that:

  1. r_hat is the Gelman-Rubin statistic

  2. The two effective sample size statistics (beginning with ess) are as discussed in the prior chapter

  3. The standard error of sampling is provided by mcse_mean

Autocorrelation Plots#

pm.plot_autocorr(trace,figsize=(17,5));
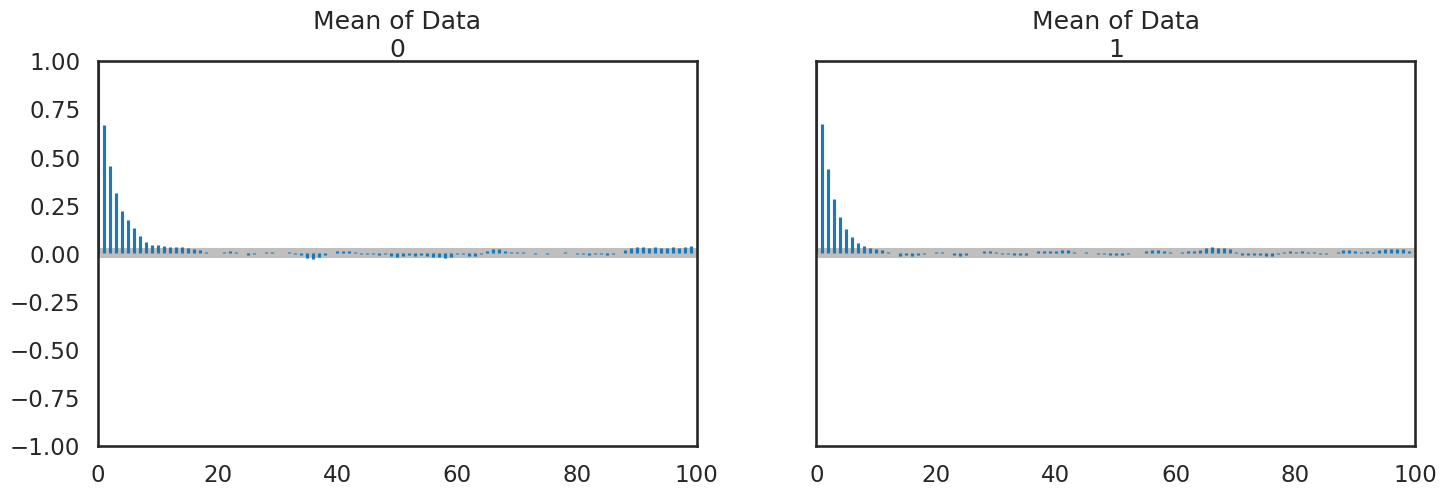
../_images/a4f58930f2cd9de44606d774fb4c59cf96d57c41be878554a66da4b64f12b2e9.png

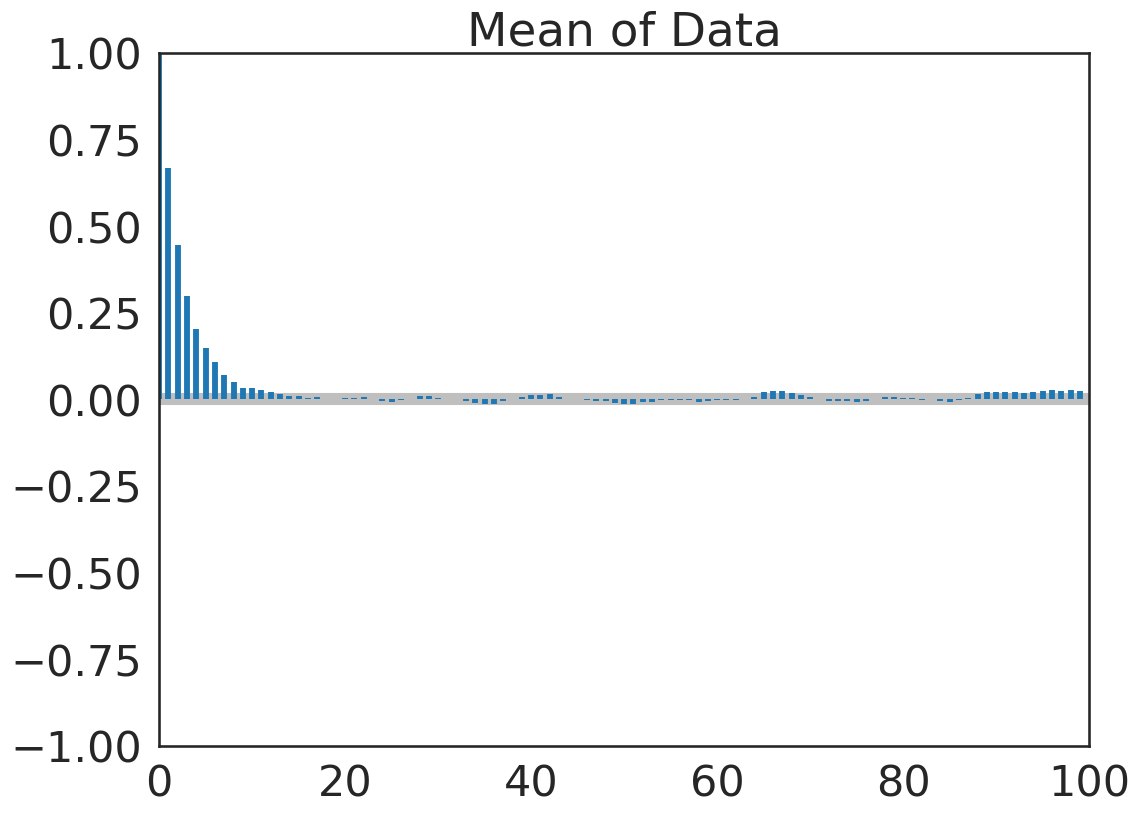
For me, this is better viewed as combined particularly after you examine the Gelman Rubin statistic and confirm convergence:

pm.plot_autocorr(trace, figsize=(12,9), combined=True);
../_images/c4aa3e841a6a7516c89721019ad21a03f4a07e811594ae5ccf61f84a51e3bbc2.png

Acceptance Rate#

The acceptance rate can also be computed from our trace object:

accept = trace.sample_stats.accepted.mean().to_numpy()
print("Acceptance Rate: ", accept.round(3))

Acceptance Rate:  0.329
Contents